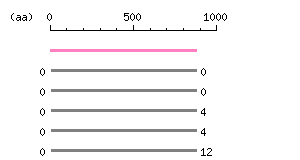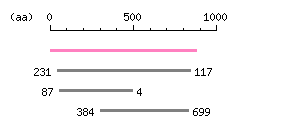Length: 3113 bp
|
| cloned DNA seq. | |
Warning for N-terminal truncation: | NO |
Warning for coding interruption: | NO |
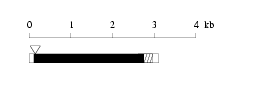
Length of 3'UTR 351 bp Genome contig ID gi65488608f_86420104 PolyA signal sequence
(AATAAA,-22)
ATCAGTGTCATGGAATAAAATCAAGTGTGAATTGCFlanking genome sequence
(446154 - 446203)
TGTCTGTGTAGATGCCATGGGCAAGCATGGCAGCTGGGTGGCCTGTCACC
KIAA Alignment based on: FLJ00327 DNA sequence, AA sequence, Physical map